Camera

If a mutable has an attribute type of camera, it’s a camera. Typically, a simple pinhole camera model is used.

Required attributes of a camera:

Name	Type
camera_parameters	dict

camera_parameters is a dictionary with the following six required keys:

Name	Type
screen_width	int
screen_height	int
focal_length	numeric
horizontal_aperture	numeric
near_clip	numeric
far_clip	numeric

Pinhole Model

3D objects are projected onto a 2D plane, like this:

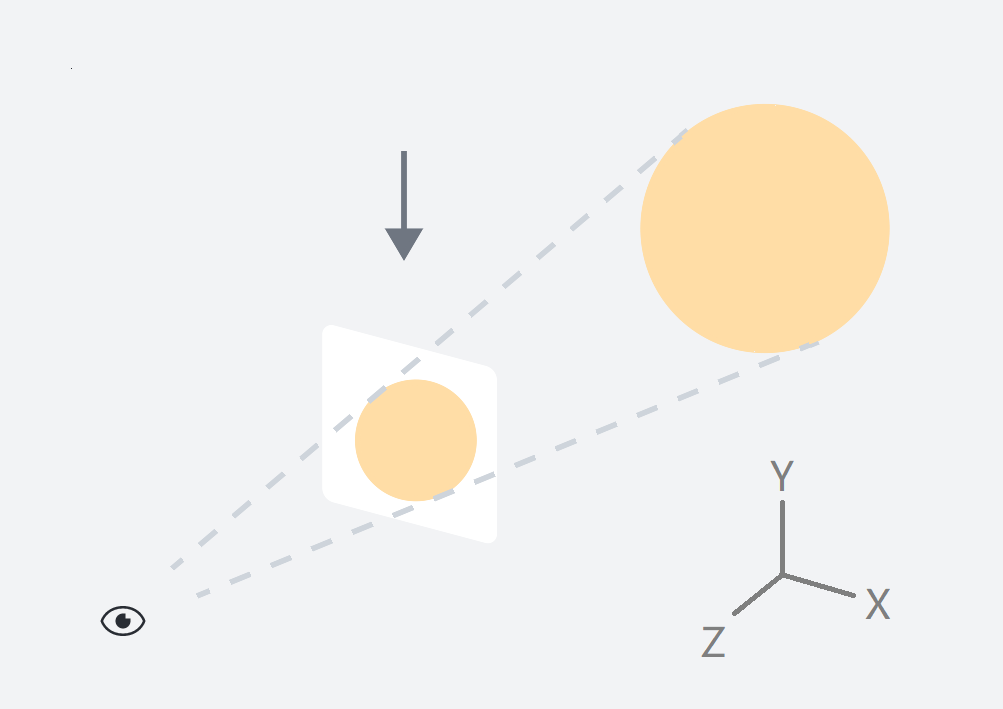
Looking from a top view, towards the negative Y-axis:

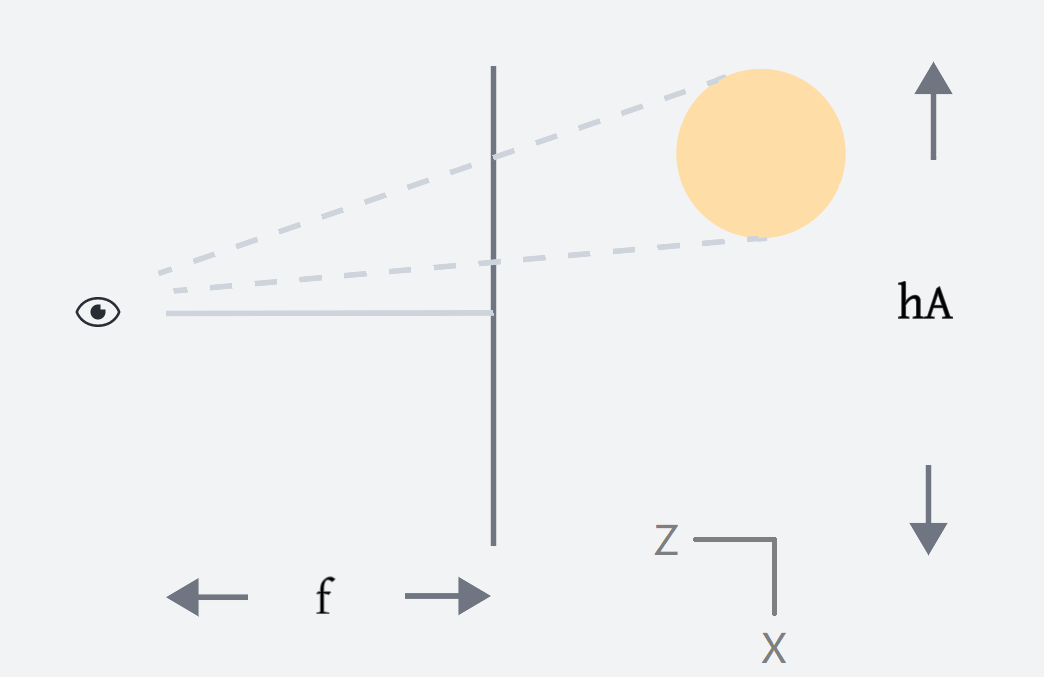
In the picture, f, which is the distance from the camera to the projection plane, is focal_length. hA is the distance from the left edge (upper end) to the right edge (lower end) and stands for horizontal_aperture.

near_clip and far_clip define two planes perpendicular to the line of vision between which you can see things.

Assumptions

The following assumptions are made in frame of reference and conversion from/to other common representations.

If no transform operator is applied on the camera, the Y-axis points upwards and X-axis points to the right. The camera looks towards negative direction of the Z-axis.

There are many standards out there for the pinhole camera. To avoid confusion, we define a value called the \(pinholeRatio\) such that \(pinholeRatio=\frac{2∗focalLength∗aspectRatio}{horizontalAperture}\)

If you are familiar with OpenGL/Direct3D, \(fovy\) is used more often.

\[pinholeRatio=\frac{1}{\tan(fovy/2)}\]

If you are familiar with the intrinsic matrix or the Objectron standard, \(fx, fy, cx, cy\) are used.

\[\begin{split}fx = \frac{screenWidth \cdot pinholeRatio}{2 \cdot aspectRatio}\\ fy = \frac{screenHeight \cdot pinholeRatio}{2}\\ cx = screenWidth / 2\\ cy = screenHeight / 2\end{split}\]

Here, \(aspectRatio = screenWidth/screenHeight\).